Объяснение контекстно-зависимого
периода полувыведения

[ Введение | Оглавление | Анализ динамики концентрации фентанила ]

  Мультиэкспоненциальные модели, описывающие фармакокинетику альфентанила, фентанила, мидазолама, пропофола и тиопентала, были взяты из опубликованных литературных данных. Эти модели иллюстрировали собой формулу распределения:

  udf(t) = A₁e^{-l (1)t} +A₂e^{-l (2)t} +A₃e^{-l (3)t} ,

  где udf(t) - это концентрация препарата в центральной камере, возникающая после единичного болюса, введенного внутривенно, и где l₁>l₂>l₃. Период полувыведения был рассчитан как ln2/l₃.
  Трехемкостная гидравлическая модель, изображенная на рис. 1, является физическим аналогом трехкамерной математической модели. Более того, дифференциальные уравнения, описывающие высоту уровня жидкости в каждой емкости, являются теми же уравнениями, которые описывают концентрацию препарата в каждой камере фармакокинетической модели. Используя гидравлическую модель, мы можем дать рациональное объяснение роли распределения в определении постинфузионной концентрации препарата в центральной камере.

Рисунок 1.

  Модель, изображенная на рис. 1, состоит из центральной емкости (емкость №1), соединенной трубами с двумя периферическими емкостями (емкость №2 и емкость №3), которые не сообщаются между собой. Объем воды в каждой емкости аналогичен количеству вещества в соответствующей камере фармакологической модели. Соответственно, и высота жидкости в каждой емкости соответствует концентрации препарата в каждой камере соответствующей многокамерной модели.
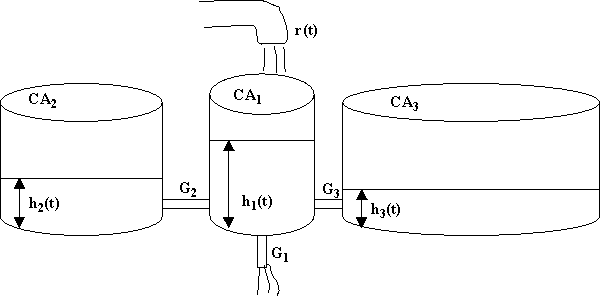
  Скорость, r(t), с которой вода вливается в емкость №1, - аналог скорости внутривенной инфузии препарата. Скорость G_i(h₁(t) - h_i(t)), с которой вода перетекает из емкости №1 в емкость №i, пропорциональна разнице уровней, h₁(t) и h_i(t), в емкости №1 и емкости №i соответственно, где G_i - это проводимость (величина обратная сопротивлению) трубы, соединяющей емкости №1 и емкость №i. Положительная величина G_i(h₁(t) - h_i(t)) означает, что жидкость перетекает из емкости №1 в емкость №i, а отрицательное величина этого параметра говорит об обратном токе жидкости (поскольку жидкость движется по градиенту давления). Вода вытекает из емкости №1 со скоростью G₁h₁(t), где G₁ - это проводимость отверстия в дне емкости №1, а h₁(t) - это уровень жидкости в емкости №1.
  Представим, что мы проводим инфузию препарата с такой скоростью, чтобы поддерживать постоянную величину h₁(t), равной H₁. Если r(t) поддерживать бесконечно долго, то, как это хорошо видно из рисунка 1, то h₂(t) и h₃(t) станут равны H₁, а G₁H₁ будет равно r(t). Очевидно, что в многокамерной фармакологической модели после достаточно долгой инфузии препарата в центральную камеру будет достигнуто устойчивое состояние, при котором концентрация препарата во всех камерах будет одинаковая.
  Динамика состояния гидравлической модели определяется проводимостями G и площадями цилиндров СА каждой из трех емкостей.

Таблица 1.
Рассчеты временных констант и соотношения
проводимостей для гидравлияческой и
фармакокинетической моделей

  Если h₁(t) поддерживать постоянной на уровне Н₁, то достижение h₂(t) и h₃(t) величины Н₁ будет зависеть только от G₂ и СА₂ и от G₃ и СА₃, соответственно. В частности, временные константы ТС₂ и ТС₃ могут быть определены, согласно таблице 1, как СА₂/G₂ и СА₃/G₃, соответственно, измеряемые в единицах времени. Предположив, что емкости №2 и №3 изначально пустые, а h₁(t) равно Н₁, то временные константы можно интерпретировать количественно равными периодам полувыведения. Например, после промежутка времени ТС₂ уровень воды в емкости №2 поднимется до высоты 63%Н₁; через время 2 ТС₂ от начала отсчета - до 86% Н₁; через 3 ТС₂ - до 95%Н₁ и т.д. Чем больше временные константы для комбинации “труба - периферическая емкость”, тем большее время потребуется для установления динамического равновесия между этой емкостью и емкостью №1.
  После прекращения инфузии, поддерживающей постоянный уровень жидкости в емкости №1, скорость снижения уровня жидкости в емкости №1 будет зависеть от двух составляющих - от процессов элиминации и перераспределения. Элиминация - это собственная способность емкости №1 необратимо опорожнять себя. Скорость элиминации является функцией площади поверхности цилиндра (СА) и проводимости отверстия в дне емкости №1. Соответственно, мы можем определить (согласно таблице 1) константу элиминации, ТС₁=СА₁/G₁. При r(t)=0, т.е отсутствии поддерживающей инфузии и отсутствии возврата жидкости из периферических емкостей, уровень воды в емкости №1 через промежуток времени ТС₁ минут после прекращения инфузии будет составлять 37%Н₁; через 2 ТС₁ он будет равен 14% ТС₁ и т.д. Итак, чем меньше ТС₁, тем быстрее снижается уровень h₁(t).
  В многокамерных моделях постинфузионная кинетика более сложная, чем в вышеприведенном примере. В частности, вода будет продолжать перемещаться в периферическую камеру до тех пор, пока h₁(t) будет больше, чем h_i(t). Продолжающийся поток воды в периферическую емкость, который происходит одновременно с вытеканием жидкости через отверстие в дне емкости №1, приведет к значительно более быстрому снижению уровня жидкости h₁(t) в постинфузионном периоде. Уровень жидкости в периферических емкостях достигнет равновесия с h₁(t) в различное время, и однажды, когда h₁(t) станет ниже, чем h_i(t), вода начнет возвращаться назад в емкость №1 со скоростью G_i(h₁(t)-h_i(t)) где i=2 или 3. Возврат жидкости из периферических емкостей назад в центральную емкость №1 выступает в роли противодействия попыткам емкости №1 при помощи проводимости G₁ снизить свой уровень жидкости. Мы считаем, что (согласно таблице 1) соотношение проводимостей G_i/G₁ -ценный показатель влияния емкости i на постинфузионную кинетику емкости №1.
  Хотя этот соотношение представляет в значительной мере упрощенное взаимодействие между емкостями и трубами, большая величина соотношения G_i/G₁ означает, что емкость №i возвращает воду назад в емкость №1 с достаточно высокой скоростью, чтобы уменьшить градиент между h_i(t) и h₁(t). Подобным образом, малая величина G_i/G₁ предполагает, что вода возвращается из емкости №i в емкость №1 столь медленно по сравнению с вытеканием воды из емкости №1 через G₁ , что в постинфузионном периоде будет сохраняться большой градиент между h_i(t) и h₁(t). Очевидно, что чем больше соотношение проводимостей, тем в большей степени уровень h₁(t) будет поддерживаться обратным током воды из периферических емкостей, а соответственно, уровень h₁(t) будет снижаться медленнее.

Таблица 2
Взаимоотношение между параметрами гидравлической
и фармакокинетической трехкамерными моделями

    Теперь мы перейдем к известной фармакологической номенклатуре (центральная камера, периферическая камера, концентрация плазмы и т. д.) в описании процессов, которые мы только что рассмотрели на примере модели с емкостями и уровнем воды. (Мы хотим отметить, что соотношение G_i/G₁ качественно и количественно равно соотношению клиренс_i/клиренс₁. Межкамерный клиренс составляет V₁k_1i=V_ik_i1, а центральный клиренс - это клиренс₁ V₁k₁₀)

Таблица 3
Объемы камер и межкамерные клиренсы

Препарат	k10 (мин-1)	k12 (мин-1)	k21 (мин-1)	k13 (мин-1)	k31 (мин-1)	V1 (l)	V2(l)	V3(l)
альфентанил	8,.946*10-2	6,540*10-1	2,089*10-1	1,179*10-1	1,775*10-2	2,2	6,9	14,6
фентанил	5,.940*10-2	3,725*10-1	9,597*10-2	1,740*10-1	6,522*10-3	13	50,4	347
мидазолам	1,651*10-2	---	---	1,895*10-2	1,003*10-2	30,9	---	58,5
пропофол	6,923*10-2	1,006*10-1	5,685*10-2	5,634*10-2	4,687*10-3	19,7	34,8	236
суфентанил	6,629*10-2	2,701*10-1	1,009*10-1	7,127*10-2	2,583*10-3	18	48,2	497
тиопентал	1,240*10-2	1,376*10-1	1,216*10-1	1,396*10-2	5,445*10-3	18,9	21,3	48,5